Infrared thermometers for non-contact temperature measurement are highly developed sensors which have wide-spread application in industrial processing and research. This paper describes, in non-mathematical terms, the theory upon which the measurement technology is based, and how this is used to deal with the variety of application parameters which confront the intending user.
Introduction
Designs for an infrared thermometer (IRT), have existed since at least the late nineteenth century, and various concepts were featured by Charles A. Darling (1) in his book "Pyrometry," published in 1911. However it was not until the 1930's that the technology was available to turn these concepts into practical measuring instruments. Since that time there has been considerable evolution in the design and a large amount of measurement and application expertise has accrued. At the present time, the technique is well accepted and is widely used in industry and in research.
Measurement Principles
As previously stated IR energy is emitted by all materials above 0°K. Infrared radiation is part of the Electromagnetic Spectrum and occupies frequencies between visible light and radio waves. The IR part of the spectrum spans wavelengths from 0.7 micrometers to 1000 micrometers (microns). Figure 1. Within this wave band, only frequencies of 0.7 microns to 20 microns are used for practical, everyday temperature measurement. This is because the IR detectors currently available to industry are not sensitive enough to detect the very small amounts of energy available at wavelengths beyond 20 microns.
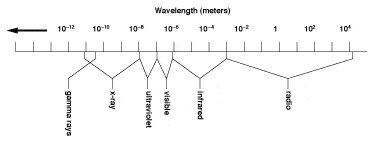INFRARED SPECTRUM 0.7 TO 1000 MICROMETERS (MICRONS)
Electromagnetic Spectrum
Though IR radiation is not visible to the human eye, it is helpful to imagine it as being visible when dealing with the principles of measurement and when considering applications, because in many respects it behaves in the same way as visible light. IR energy travels in straight lines from the source and can be reflected and absorbed by material surfaces in its path. In the case of most solid objects which are opaque to the human eye, part of the IR energy striking the object's surface will be absorbed and part will be reflected. Of the energy absorbed by the object, a proportion will be re-emitted and part will be reflected internally. This will also apply to materials which are transparent to the eye, such as glass, gases and thin, clear plastics, but in addition, some of the IR energy will also pass through the object. The foregoing is illustrated in Figure 2. These phenomena collectively contribute to what is referred to as the Emissivity of the object or material.
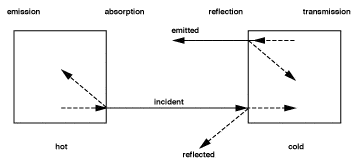RADIATIVE HEAT EXCHANGE
Materials which do not reflect or transmit any IR energy are known as Blackbodies and are not known to exist naturally. However, for the purpose of theoretical calculation, a true blackbody is given a value of 1.0. The closest approximation to a blackbody emissivity of 1.0, which can be achieved in real life is an IR opaque, spherical cavity with a small tubular entry as shown in Figure 3. The inner surface of such a sphere will have an emissivity of 0.998.
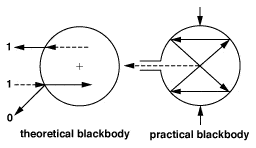EMISSIVITY
Different kinds of materials and gases have different emissivities, and will therefore emit IR at different intensities for a given temperature. The emissivity of a material or gas is a function of its molecular structure and surface characteristics. It is not generally a function of color unless the source of the color is a radically different substance to the main body of material. A practical example of this is metallic paints which incorporate significant amounts of aluminum. Most paints have the same emissivity irrespective of color, but aluminum has a very different emissivity which will therefore modify the emissivity of metallized paints.
Just as is the case with visible light, the more highly polished some surfaces are, the more IR energy the surface will reflect. The surface characteristics of a material will therefore also influence its emissivity. In temperature measurement this is most significant in the case of infrared opaque materials which have an inherently low emissivity. Thus a highly polished piece of stainless steel will have a much lower emissivity than the same piece with a rough, machined surface. This is because the grooves created by the machining prevent as much of the IR energy from being reflected. In addition to molecular structure and surface condition, a third factor affecting the apparent emissivity of a material or gas is the wavelength sensitivity of the sensor, known as the sensor's spectral response. As stated earlier, only IR wavelengths between 0.7 microns and 20 microns are used for practical temperature measurement. Within this overall band, individual sensors may operate in only a narrow part of the band, such as 0.78 to 1.06, or 4.8 to 5.2 microns, for reasons which will be explained later.
Theoretical Basis for IR Temperature Measurement
The formulas upon which infrared temperature measurement is based are old, established and well proven. It is unlikely that most IRT users will need to make use of the formulas, but a knowledge of them will provide an appreciation of the interdependency of certain variables, and serve to clarify the foregoing text. The important formulas are as follows:
- Kirchoff's Law When an object is at thermal equilibrium, the amount of absorption will equal the amount of emission.
- Stephan Boltzmann Law The hotter an object becomes the more infrared energy it emits.
- Wien's Displacement Law The wavelength at which the maximum amount of energy is emitted becomes shorter as the temperature increases.
- Planck's Equation Describes the relationship between spectral emissivity, temperature and radiant energy.
Infrared Thermometer Design and Construction
A basic infrared thermometer (IRT) design, comprises a lens to collect the energy emitted by the target; a detector to convert the energy to an electrical signal; an emissivity adjustment to match the IRT calibration to the emitting characteristics of the object being measured; and an ambient temperature compensation circuit to ensure that temperature variations within the IRT, due to ambient changes, are not transferred to the final output. For many years, the majority of commercially available IRT's followed this concept. They were extremely limited in application, and in retrospect did not measure satisfactorily in most circumstances, though they were very durable and were adequate for the standards of the time. Such a concept is illustrated in Figure 4.
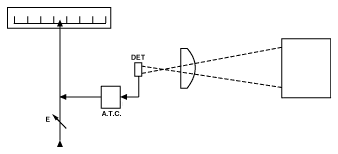Infrared Temperature Measurement
The modern IRT is founded on this concept, but is more technologically sophisticated to widen the scope of its application. The major differences are found in the use of a greater variety of detectors; selective filtering of the IR signal; linearization and amplification of the detector output; and provision of standard, final outputs such as 4-20mA, 0-10Vdc, etc. Figure 5 shows a schematic representation of a typical contemporary IRT. Probably the most important advance in infrared thermometry has been the introduction of selective filtering of the incoming IR signal, which has been made possible by the availability of more sensitive detectors and more stable signal amplifiers. Whereas the early IRT's required a broad spectral band of IR to obtain a workable detector output, modern IRT's routinely have spectral responses of only 1 micron. The need to have selected and narrow spectral responses arises because it is often necessary to either see through some form of atmospheric or other interference in the sight path, or in fact to obtain a measurement of a gas or other substance which is transparent to a broad band of IR energy.
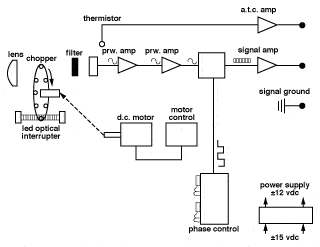MODERN INFRARED THERMOMETER
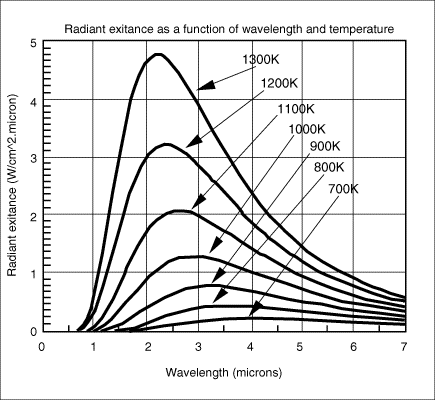
Some common examples of selective spectral responses are 8-14 microns, which avoids interference from atmospheric moisture over long path measurements; 7.9 microns which is used for the measurement of some thin film plastics; and 3.86 microns which avoids interference from CO2 and H2O vapor in flames and combustion gases. The choice between a shorter, or longer wavelength spectral response is also dictated by the temperature range because, as Planck's Equation shows, the peak energy shifts towards shorter wavelengths as the temperature increases. The graph in Figure 6 illustrates this phenomenon. Applications which do not demand selective filtering for the above stated reasons may often benefit from a narrow spectral response as close to 0.7 microns as possible. This is because the effective emissivity of a material is highest at shorter wavelengths and the accuracy of sensors with narrow spectral responses is less affected by changes in target surface emissivity.
It will be apparent from the foregoing information that emissivity is a very important factor in infrared temperature measurement. Unless the emissivity of the material being measured is known, and incorporated into the measurement, it is unlikely that accurate data will be obtained. There are two methods for obtaining the emissivity of a material:
a) by referring to published tables and b) by comparing the IRT measurement with a simultaneous measurement obtained by a thermocouple or resistance thermometer and adjusting the emissivity setting until the IRT reads the same. Fortunately, the published data available from the IRT manufacturers and some research organizations is extensive, so it is seldom necessary to experiment. As a rule of thumb, most opaque, non-metallic materials have a high and stable emissivity in the 0.85 to 9.0 range; and most un-oxidized, metallic materials have a low to medium emissivity from 0.2 to 0.5, with the exception of gold, silver and aluminum which have emissivities in the order of 0.02 to 0.04 and are, as a result, very difficult to measure with an IRT. While it is almost always possible to establish the emissivity of the basic material being measured, a complication arises in the case of materials which have emissivities that change with temperature such as most metals, and other materials such as silicon and high purity, single crystal ceramics. Some applications which exhibit this phenomenon can be solved using the two color, ratio method.
Two Color-Ratio Thermometry
Given that emissivity plays such a vital role in obtaining accurate temperature data from infrared thermometers, it is not surprising that attempts have been made to design sensors which would measure independently of this variable. The best known and most commonly applied of these designs is the Two Color-Ratio Thermometer. This technique is not dissimilar to the infrared thermometers described so far, but measures the ratio of infrared energy emitted from the material at two wavelengths, rather than the absolute energy at one wavelength or wave band. The use of the word "color" in this context is somewhat outdated, but nevertheless has not been superseded. It originates in the old practice of relating visible color to temperature, hence "color temperature."
The basis for the effectiveness of two-color thermometry is that any changes in either the emitting property of the material surface being measured, or in the sight path between the sensor and the material, will be "seen" identically by the two detectors, and thus the ratio and therefore the sensor output will not change as a result. Figure 7 shows a schematic representation of a simplified two-color thermometer.
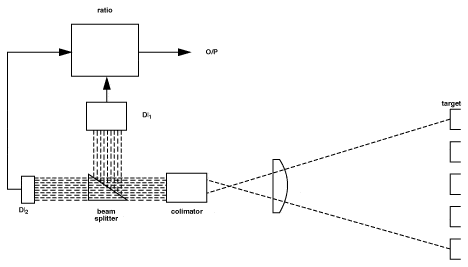TWO COLOR THERMOMETRY(Ratio Thermometry)
Because the ratio method will, under prescribed circumstances, avoid inaccuracies resulting from changing or unknown emissivity, obscuration in the sight path and the measurement of objects which do not fill the field of view, it is very useful for solving some difficult application problems. Among these are the rapid induction heating of metals, cement kiln burning zone temperature and measurements through windows which become progressively obscured, such as vacuum melting of metals. It should be noted however, that these dynamic changes must be "seen" identically by the sensor at the two wavelengths used for the ratio, and this is not always the case. The emissivity of all materials does not change equally at two different wavelengths. Those materials that do are called "Greybodies." The ones that do not are called "Non-Greybodies." Not all forms of sight path obscuration attenuate the ratio wavelengths equally either. The predominance of particulates in the sight path which are the same micron size as one of the wavelengths being used will obviously unbalance the ratio. Phenomena which are non-dynamic in nature, such as "non-greybody" material, can be dealt with by biasing the ratio, an adjustment referred to as "Slope." However, the appropriate slope setting must generally be arrived at experimentally. Despite these limitations, the ratio method works well in a number of well-established applications, and in others is the best, if not the most preferred solution.
Summary
Infrared thermometry is a mature but dynamic technology that has gained the respect of many industries and institutions. It is an indispensable technique for many temperature measurement applications, and the preferred method for some others. When the technology is adequately understood by the user, and all the relevant application parameters are properly considered, a successful application will usually result, providing the equipment is carefully installed. Careful installation means ensuring that the sensor is operated within its specified environmental limits, and that adequate measures are taken to keep the optics clean and free from obstructions. A factor in the selection process, when choosing a manufacturer, should be the availability of protective and installation accessories, and also the extent to which these accessories allow rapid removal and replacement of the sensor for maintenance. If these guidelines are followed, the modern infrared thermometer will operate more reliably than thermocouples or resistance thermometers in many cases.
References
Darling, Charles R.; "Pyrometry. A Practical Treatise on the Measurement of High Temperatures." Published by E.&F.N. Spon Ltd. London. 1911.
Author and Presenter: John Merchant, Sales Manager, Mikron Instrument Company Inc.
What is a Calibrator and why is it an important device? Introduction to Instrument Calibration
